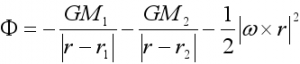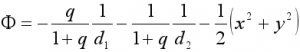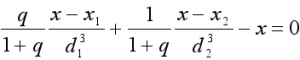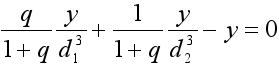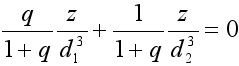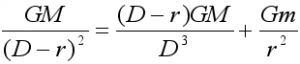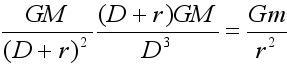[hidepost=0]Article paru dans PROCYON n°146[/hidepost]

Introduction

Joseph-Louis de Lagrange est un mathématicien né en Italie mais considéré comme un mathématicien français. Il a découvert ce qu’on appellera plus tard les 5 points de Lagrange vers les années 1770, et ceci en même temps que le mathématicien suisse Euler, sans jamais avoir eu de contact direct avec lui si ce n’est épistolaire.

Exposer les points de Lagrange sans entrer un peu dans des mathématiques n’est pas possible, mais j’essaierai d’être le plus clair possible.

La théorie fondamentale est simple : les points de Lagrange sont des points d’équilibre gravitationnel (dans un système à 3 corps) pour un corps à masse faible dans un ensemble de 2 corps à masse importante. Cette situation n’a pas l’apanage du système solaire et peut se retrouver n’importe où, même au niveau des galaxies.

La solution élégante

L’étude du potentiel de Roche, tiré d’une étude sur les systèmes binaires (d’étoiles) permet de trouver « facilement » les points de Lagrange, [1].

Dans le cas d’un système d’étoiles doubles, le potentiel de Roche est la somme du potentiel gravitationnel dû aux deux masses et du potentiel centrifuge, car les 2 étoiles tournent l’une autour de l’autre.

Ce potentiel Ф s’écrit :

(1)

où G est la constante gravitationnelle, ω est la vitesse angulaire du système, M₁ et M₂ sont les masses des 2 étoiles, r₁ et r₂ sont les positions des 2 étoiles, dont la séparation orbitale est a.

Figure 1

On choisit maintenant un repère (un système d’axes) ayant pour origine le centre de gravité du système : l’axe z est perpendiculaire au plan de l’orbite, les 2 masses sont situées sur l’axe des x, aux positions et   où , les distances étant normalisées par la séparation orbitale a.

Dans ce repère et avec la normalisation définie ci-dessus, le potentiel Ф s’écrit :

(2)

où et .

Le potentiel Ф est normalisé par .

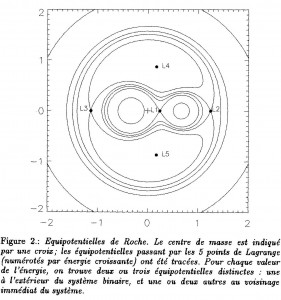
On peut maintenant tracer les équipotentielles (Ф = constante) comme on peut le voir sur la figure 1 (qui est la figure 2 tirée de la référence [1]).

Cette figure met en évidence les 5 points de Lagrange, points pour lesquels le gradient du potentiel est nul, c’est-à-dire Φ=0. Comme le gradient s’écrit (d / dx, d / dy, d / dz), on va obtenir 3 équations qui s’écrivent :

(3)

(4)

(5)

La dernière équation a une solution évidente  z=0, ce qui nous dit que les points de Lagrange sont situés dans le plan orbital. L’équation (4) admet plusieurs solutions et la première est évidente y=0, ce qui entraîne pour l’équation (3) une simplification. Elle devient :

(6)

où S₁et S₂ sont les signes de x-x₁et x-x₂ respectivement.

Cette équation admet 3 solutions (L1,L2,L3) et dans la remarque qui va suivre on appliquera la solution au cas de l’ensemble Terre-Soleil. On peut montrer que ces 3 points sont instables, car la figure 1 montre que les lignes équipotentielles se croisent en ces points.

L’équation (4), outre la solution y = 0 déjà exploitée, a encore 2 autres solutions, qui donnent les points de Lagrange L4 et L5. En effet, on peut très facilement vérifier que le système d’équations (3,4,5) est vérifié pour d₁ = d₂ = 1. En effet, l’équation (5) étant toujours éliminée, l’équation (4) donne qy – qy+y-y = 0, ce qui fait 0=0, enfin l’équation (3) donne –qx₁-x₂ = 0, ce qui donne encore 0=0, avec la définition de q.

Ceci place les points L4 et L5 aux sommets de 2 triangles équilatéraux ayant comme base la distance orbitale entre les corps. De plus ces 2 points sont stables car ils se trouvent à l’intérieur d’une zone close dans le tracé des équipotentielles de la figure 1, et ceci est vrai si le rapport M₁/M₂ est supérieur à une valeur critique de l’ordre de 25.

Remarque : application au système Terre-Soleil

L’axe ci-dessus présente la position (non à l’échelle) des divers points : x₁ est la position du soleil, x₀ celle du centre de gravité, x₂ celle de la terre. L’équation (6), après réduction au même dénominateur, s’écrit :

(7)

Cette équation doit se résoudre numériquement en distinguant les 3 cas possibles : 1) x<x₁ , 2) x₁<x<x₂ , 3) x>x₂ .

Avec x₁ = -0.300353*10^-7 et x₂ = 0.999996996, on trouve pour la première solution, x=-1; pour la 2^ème, on obtient x = 0.9899999939, et pour la dernière on a x = 1.0099999343.

En ramenant les solutions à la distance Terre-Soleil D=150M km (M = 10⁺⁶), on obtient : X_L3= -150 M km par rapport à la position du Soleil, X_L1= -1.5M km par rapport à la position de la Terre, et X_L2= +1.49999M km . On verra par la suite que ces valeurs sont voisines de celles qu’on trouvera par la méthode plus « hard ».

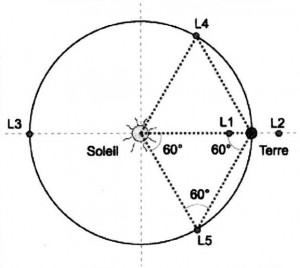
La figure 2 vous montre la position des différents points.

Figure 2

La solution « hard » pour le système Terre-Soleil

En fait cette méthode est aussi basée indirectement sur la théorie exposée plus haut, mais on s’y prend différemment pour avoir les solutions.

On va supposer que le centre de gravité du système Soleil-Terre est confondu avec le soleil, et ainsi la trajectoire de la terre autour du soleil est circulaire. De plus on supposera dans certaines formules que la masse de la terre négligeable. On va aussi supposer que l’on sait déjà qu’il y a 5 points de Lagrange et que l’on connaisse leur position approximative par rapport à la terre et au soleil.

On va considérer que la terre est dans une situation d’équilibre entre la force d’attraction du soleil et la force centrifuge engendrée par le mouvement circulaire de la terre autour du soleil. On a ainsi l’équation suivante :

(8)

avec G = la constante de gravitation universelle = 6.67*10^-11, M = la masse du soleil en kg = 1.989*10⁺³⁰, D = la distance Terre-Soleil = 150*10⁺⁹ en mètres, V = la vitesse de la Terre en m/s.

On va supposer l’existence d’un objet de masse négligeable situé en ce point d’équilibre, qui est donc le point L1, et on va calculer la position de ce point.

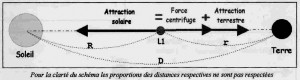
Figure 3

L’objet de masse négligeable, placé en L1, se déplace avec à la même vitesse angulaire que la terre et il sera soumis à la force centrifuge et aux attractions de la terre et du soleil. On aura l’équation suivante :

(9)

avec les distances R et r définies sur la figure 3 et m = la masse de la terre = 6.10²⁴ kg. La force centrifuge V²/R doit être écrite différemment ; en effet la vitesse V du point L1 est égale à la circonférence parcourue (2πR) divisée par la période, qui est la même que celle de la terre, et qui avec la 3^ème loi de Keppler s’écrit

. De ce fait V²/R devient RGM/D³ et l’équation (9) s’écrit comme suit avec R = D – r :

(10) .

En explicitant les différentes grandeurs de l’équation (10) et en faisant une résolution numérique on trouve r = 1 495 000 km, ce qui proche de la solution précédente (1 500 000 km).

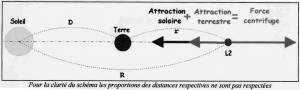
La figure 4 présente le schéma pour le calcul de L2.

Figure 4

Un objet sans masse placé en L2 circule à la même vitesse angulaire que la terre ; il est soumis à 3 forces, comme le montre la figure 4 : la force centrifuge, l’attraction de la terre et celle du soleil. Dans le cas présent, l’objet serait entraîné loin de la terre si les attractions de la terre et du soleil ne le maintenait pas près de la terre, si bien qu’on obtient la relation : attraction du soleil + attraction de la terre = la force centrifuge :

(11) .

Avec les mêmes calculs que précédemment pour le terme vitesse, on arrive à l’équation suivante :

(12) .

Avec la résolution numérique, on trouve r = 1 502 000 km, ce qui est voisin de la solution précédente (1 499 999 km). Les légères différences entre les solutions tiennent surtout au fait que les hypothèses de départ ne sont pas exactement les mêmes ( le centre de gravité est correct dans le premier cas et confondu avec le soleil dans le 2^ème cas) et que la résolution numérique reste toujours une approximation.

Pour les autres points de Lagrange, L1, L4 et L5, il n’y a pas de solution qui soit évidente à présenter (plusieurs pages pour L4 et L5 dans la référence [2]). Aussi, on s’en tiendra donc à la solution trouvée dans le premier paragraphe.

Conclusion

Sur Internet, on trouve beaucoup de solutions qui aboutissent à la position des points de Lagrange. Certaines sont vraiment laborieuses comme la référence [2,3].

J’espère vous avoir bien expliqué les points de Lagrange qui existent pour n’importe quel système de 2 astres massifs et d’un troisième à masse négligeable.

Remerciements

Je remercie Monsieur Jean-Marie Hameury de l’Observatoire de Strasbourg pour l’aide qu’il a apportée dans la rédaction de cet article avec sa publication citée en référence [1].

Bibliographie

[1] Jean-Marie Hameury, Géométrie de Roche dans les systèmes binaires serrés, Observatoire de Strasbourg

[2] Sciences.ch, Histoire de la Cosmologie.

[3] Les points de Lagrange par Jean-Pierre Martin, sur www.planetastronomy.com