Dans le cadre de l’Année Mondiale de l’Astronomie (AMA09), le groupe des littéraires de la première L/ES du lycée Alfred Kastler de Guebwiller, à l’initiative de leur professeur de Mathématiques, M. Philippe, a reproduit l’expérience du philosophe et homme de science grec Eratosthène. Rappelons que cette expérience permet de donner une estimation de la circonférence polaire de la Terre. Les résultats définitifs ayant été connus peu avant Pâques, voici le compte-rendu de cette aventure astronomique.
L’Expérience au IIIème siècle avant J-C
Eratosthène de Cyrène est un philosophe et un homme de science de l’Antiquité grecque. Les historiens le situent entre 284 et 192 av. J-C. Outre le méridien terrestre, il est également le créateur du crible des nombres premiers.
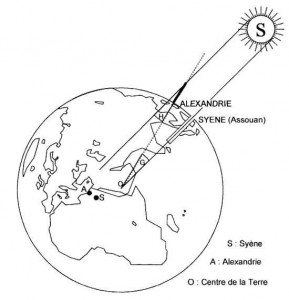
Le scientifique s’est aperçu qu’au solstice d’été le Soleil se mire au fond d’un puits à Syène mais que l’obélisque d’Alexandrie projette une ombre. Il sait donc que le Soleil est au zénith à Syène mais pas à Alexandrie. Il mesure alors l’ombre de l’obélisque. Il trouve un huitième de la hauteur totale.
Rappelons qu’à l’époque d’Eratosthène, le zéro ainsi que la trigonométrie sont inconnus. Son expérience est soumise à plusieurs conditions :
- un postulat selon lequel les rayons du Soleil, du fait de son éloignement, nous arrivent parallèlement
- une certitude : la Terre est ronde
- trois supposés : Syène et Alexandrie sont sur le même méridien ; sont séparées par cinq mille stades égyptiens ; Syène se situe sur le tropique du Cancer.
Pour réaliser son expérience, Eratosthène se sert d’une règle, du Soleil et d’un gnomon, qui sera l’obélisque. Le raisonnement d’Eratosthène peut se traduire par ce schéma :
Par la propriété des angles alternes-internes : G = H. Eratosthène s’aperçoit que l’angle H est égal à 1/50 de la circonférence totale. Il ne lui restait plus qu’à multiplier par cinquante la distance Syène – Alexandrie. Il obtient une circonférence de 25 000 stades égyptiens, soit environ 39 500 km. Actuellement, la circonférence polaire de la Terre est estimée à 39 940 km.
C’est une expérience et un calcul similaires qu’ont réalisés les élèves du Lycée Alfred Kastler.
L’Expérience au XXIème siècle après J-C
A l’origine, le « projet Eratosthène » devait être réalisé en partenariat avec le lycée Sainte-Marie de Cannes. Mais les correspondants ne s’étant pas manifestés dans les délais, seul M. Bernard Berri, membre du CAW réalisa l’expérience à Cannes.
On décida de prendre pour repère, en lieu de Syène et Alexandrie, Guebwiller et Cannes, qui se trouvent approximativement sur le même méridien.
Le premier travail consista à estimer la distance géodésique séparant Guebwiller et Cannes. Après un premier travail « raté », le calcul effectué avec dix-huit valeurs a donné les résultats suivants :
- Une moyenne µ de 478,7 km
- Un écart-type σ de 8,8 km
- Un intervalle de confiance situé entre 466 et 492 km.
Deux valeurs aberrantes furent ôtées du calcul. La moyenne retenue est alors de 482 km entre Guebwiller et Cannes.
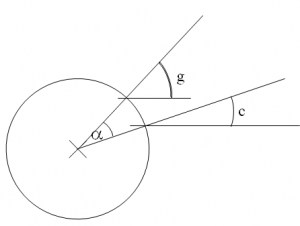
Il fallut ensuite expliquer la différence de latitude entre Guebwiller et Cannes (voir schéma 2). On en déduisit que l’angle α au centre de la Terre était égal à g – c.
Nous pouvions dès lors procéder à l’expérience. Restait à attendre un temps dégagé…
Documents :
g : angle zénithal à Guebwiller
α : angle au centre de la Terre
c : angle zénithal à Cannes
Journée du 17 mars 2009 et résultats
L’expérience débuta à 8h30. Sur les dix-neuf gnomons installés, dix-sept furent jugés fiables. Tout au long de la journée, les responsables des gnomons marquèrent à la craie, tous les quarts d’heure, l’extrémité de l’ombre projetée au sol (voir schéma 3). Le Soleil fut présent tout au long de l’expérience. On cessa de marquer les ombres vers 13h30, le méridien étant dépassé. Nous nous sommes trouvés face à un cas particulier. En raison de la proximité avec l’équinoxe de printemps (21 mars), les différents points marqués au sol étaient alignés. L’ombre la plus courte était celle de 12h45 environ, moment où le Soleil culminait au Sud.
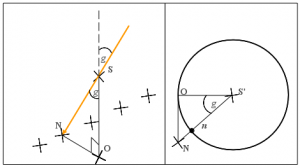
Pour estimer l’angle du Soleil à la verticale, nous avons projeté au sol le triangle ONS’ déterminé par : O le point de station du gnomon, OS’ sa longueur et N le point correspondant à celui de l’ombre la plus courte. Ce triangle est rectangle en O.
Nous avons ensuite tracé l’arc de cercle tangent en O à partir du centre S’ (voir schéma 4). Grâce à une ficelle, nous avons mesuré la longueur de l’arc On et finalement estimé l’angle g en tour, comme étant : On / périmètre du cercle. Nous avons gardé quatre décimales, ce qui correspond à la précision du dixième de degré environ. Nous n’avons réalisé aucun calcul savant en trigonométrie, ni utilisé un rapporteur qui finalement aurait été moins précis.
La moyenne µ des angles, calculée sur Excel® donna 0,1323 tour, l’écart-type σ était de 0,0126 tour. L’intervalle de confiance se situait entre 0,1135 et 0,1512 tour. Trois résultats hors de cet intervalle furent à nouveau écartés. La nouvelle moyenne retenue est de 0,1343 tour.
Nous avons ensuite pris connaissance de la mesure de l’angle zénithal à Cannes effectuée par M. Bernard Berri : soit 0,1208 tour.
On en déduit que l’angle α au centre de la Terre était égal à : 0,1343 – 0,1208 soit 0,0135 tour.
Sachant que 0,0135 tour correspond à 482 km, un tour correspondrait donc à 482 / 0,0135 soit 35 704 km. Le résultat final retenu est donc un tour polaire mesurant environ 35 704 km.
Mais le résultat d’une expérience n’étant jamais rigoureusement exact nous avons voulu estimer notre marge d’erreur. Actuellement, le méridien terrestre est estimé de façon plus précise à 39 940 km. Nous avons donc commis une erreur de 4 236km, soit un résultat 7% en-deçà de la réalité.
Cependant, ce résultat reste honorable car Apamée, autre mathématicien grec, lorsqu’il refit l’expérience trouva 18 000 stades. Cette mesure fut reprise par Ptolémée puis dans les cartes de Christophe Colomb, or il manquait dix mille kilomètres.
Documents :
Une journée à Strasbourg
En guise de récompense, une sortie à Strasbourg a été proposée aux élèves de la classe 1L/ES ainsi qu’aux premières L1. Cette sortie, le jeudi 17 mars 2009, fut l’occasion de visiter l’horloge astronomique de la cathédrale de Strasbourg ainsi que le planétarium, la crypte aux étoiles et l’observatoire.
Conclusion
Cette journée à Strasbourg fut très enrichissante et en majorité très appréciée. Elle a démontré efficacement à des élèves dont la filière ne met pas l’accent sur les mathématiques que celles-ci peuvent être utiles au quotidien et qu’elles ne sont pas uniquement une science abstraite.
Que soient ici remerciés : M. Philippe André, initiateur du projet, pour sa persévérance et son enthousiasme communicatif ; M. Berri Bernard, qui a réalisé les mesures à Cannes, nous a présenté le principe de l’expérience replacé dans le contexte philosophique de l’époque et s’est joint à nous à Strasbourg ; ainsi que toutes les personnes ayant rendu cette expérience et cette sortie possibles.
Camille Jouan 1L/ES