Dans notre association, nous avons des astronomes amateurs qui réussissent à mesurer de vrais transits d’exoplanètes. Et ces mesures sont d’une telle qualité, qu’elles sont intégrées à une base de données professionnelle : lire l’article de Matthieu Bachschmidt, le principal acteur du CAW en ce domaine.
Récemment, des élèves scolarisés en classe de Mathématiques Spéciales (année qui suit la célèbre classe de « Math Sup ») ont fait appel à nous pour les aider dans leur travail. Il s’agit d’un TIPE sur les transits d’exoplanètes. Les deux élèves, Nastassja LABORIE et Maxime SCHLIENGER, sont même venus assister à une de nos réunions et nous ont posé plusieurs questions fort intéressantes. Parmi ces questions, il y en avait une qui m’a particulièrement stimulé. Comment obtenir une courbe théorique d’un transit d’exoplanètes ? J’ai montré à plusieurs membres du CAW les travaux qu’avaient réalisés les deux élèves de prépa. C’est alors que Luc Arnold m’a brièvement expliqué la méthode qu’il avait utilisée lui pour obtenir une courbe théorique par une méthode numérique. J’ai essayé moi aussi de faire un tel travail, toutes proportions gardées, car je ne suis pas un professionnel comme Luc, mais un amateur. C’est ce que je vais tenter de présenter ci-dessous, sous le contrôle de l’œil expert de Luc.
Dans cet article, je vais donc d’abord simplement mentionner la méthode la plus « grossière » d’obtention de cette courbe théorique. Puis, je vais montrer comment on peut obtenir un modèle numérique de disque stellaire, avec possibilité de simuler la présence de taches stellaires. Je montrerai ensuite l’aspect des courbes données par la simulation. Puis, je vais montrer l’aspect d’une courbe que donnerait des passages devant l’étoile d’une forme plus exotique. Enfin, pour finir, on verra à quoi peuvent servir de tels travaux et comment ils peuvent permettre d’obtenir des données sur un transit réel qui a été mesuré à l’aide d’un instrument, en comparant la courbe mesurée et celle obtenue par simulation numérique.
1) Méthode « grossière » pour obtenir la courbe théorique d’un transit d’exoplanète
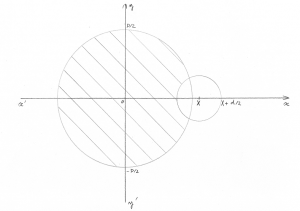
Soit une étoile symbolisée par un disque de diamètre D.
Soit une exoplanète symbolisée par un disque de diamètre d.
On peut par exemple prendre D=10d, ce qui constitue déjà une très grosse planète par rapport à une étoile. Ce n’est pas le cas sur le schéma ci-dessous.
Il suffit alors de calculer la fonction A(X) qui est l’aire hachurée sur la figure ci-dessus. C’est l’aire de la partie du disque stellaire qui n’est pas masquée par le disque planétaire. La variable X est l’abscisse de la position du centre du disque planétaire par rapport au centre du disque stellaire qui sera pris comme centre du repère. On remarquera que si X>(D+d)/2 ou si X<-(D+d)/2, A(X) sera égale à l’aire totale du disque stellaire, c’est-à-dire A=πD²/4.
Cette méthode marche très bien et l’on peut exprimer A(X) en fonction de X, D et d, à l’aide de simples fonctions trigonométriques. Seulement, elle présente un inconvénient : on considère que la surface de l’étoile a une intensité lumineuse constante par unité de surface. Résultat : la courbe de lumière ainsi obtenue a un « fond plat », comme celle montrée au début de l’article de Matthieu.
Notons que c’est ce modèle de courbe théorique qu’ont pris Nastassja LABORIE et Maxime SCHLIENGER dans leur TIPE.
Le problème qui fait que ce modèle est trop simpliste vient du fait que quand on observe un disque stellaire, il y a toujours un assombrissement en allant du centre vers le bord. Cela fait qu’une courbe réelle de lumière d’un transit d’exoplanète n’a jamais un fond plat (voir la courbe mesurée par Matthieu).
2) Créer un modèle numérique d’étoile tenant compte de l’assombrissement centre bord des disques stellaires
Comme nous venons de le dire, un disque stellaire est plus brillant au centre qu’au bord.
Cliquer ici pour voir une image en exemple (voir deuxième image de la page).
Or, il se trouve que la loi donnant l’intensité lumineuse surfacique d’une étoile en fonction de la distance au centre du disque stellaire est connue.
Cette page Wikipedia nous donne cette loi pour une étoile de type solaire.
Faisons un schéma reprenant le principe de cette page, et transformons un peu cette loi pour pouvoir l’utiliser dans notre simulation.
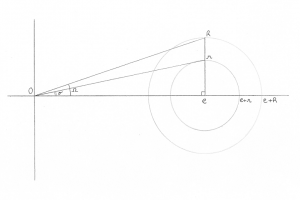
Sur le Schéma ci-dessus, l’observateur est placé en O. Vu depuis ce point O, le disque stellaire a un rayon R. On considère une couronne de ce disque de rayon r. Cette couronne a une intensité lumineuse surfacique constante. On la voit avec un angle θ par rapport au centre du disque stellaire, comme indiqué sur le Schéma. On pourrait être tenté de placer l’angle droit non pas là où l’on peut le voir sur ce schéma, mais au-dessus (en r et en R). Ceci dit, il est bien placé, car il ne faut pas oublier qu’en toute rigueur, le point O d’observation devrait être placé au-dessus du disque, à la verticale du centre du disque ici placé en abscisse e, un peu à l’emplacement de l’œil de la personne qui regarde ce schéma sur son écran d’ordinateur en lisant cet article. Cette abscisse e est en fait la distance entre l’observateur et le centre du disque stellaire.
La page Wikipedia nous donne la loi de diminution de l’intensité lumineuse des couronnes successives par unité de surface en fonction de l’angle θ :
Si nous tapons cette formule à l’aide de la notation utilisée dans le logiciel de calcul formel Mathematica, cette expression est certes bien moins lisible, mais c’est bien sous cette forme qu’on va la retrouver plus loin dans les lignes de code du programme de la simulation, en couleur bleue :
I(θ)=I(0)*(0.3 + 0.93*Sqrt[(Cos[θ])^2 – (Cos[Ω])^2]/Sin[Ω] – 0.23*((Cos[θ])^2 – (Cos[Ω])^2)/(Sin[Ω]^2))
I(0) est l’intensité maximale pour θ=0, au centre du disque stellaire.
La fonction « Sqrt » extrait la racine carrée de la quantité immédiatement entre crochets après.
Les fonctions trigonométriques sont données en notation Mathematica : « Cos » pour le cosinus, « Sin » pour le sinus, « ArcTan » pour arctangente…
Mais, ici, on a une intensité lumineuse en fonction de l’angle θ, qui vaut 0 pour le centre de l’étoile et Ω pour son bord.
On veut exprimer cette intensité lumineuse en fonction du rayon r de la couronne considérée, r variant de 0 au centre du disque stellaire, à R en son bord.
Le schéma ci-dessus montre que :
θ=ArcTan(r/e)
Ω=ArcTan(R/e)
Dans les calculs plus bas, nous prendrons un rapport de e/R de l’ordre de grandeur de 200, car il faut bien en fixer un et autant prendre à peu près le rapport réel pour le Soleil vu depuis la Terre. Ceci dit, ce rapport est vraiment beaucoup plus grand quand il s’agit d’une étoile autre que le Soleil vue depuis la Terre. S’il y a un point faible dans le travail que je présente ici, il doit certainement être là, ainsi que dans mon interprétation de la loi d’assombrissement centre-bord de l’intensité lumineuse sur un disque solaire.
Voici ci-dessous les quelques lignes qui créent l’étoile numérique en tenant compte de la loi de l’assombrissement centre-bord du disque stellaire. Ce petit programme est écrit dans le langage en usage dans le logiciel de calcul formel Mathematica. On définit au départ une matrice de taille 30×30 (variable « t »). Le diamètre de l’étoile sera de 20 (variable « etoile ») et celui de la planète de 4 (variable « planete »). On considère ici l’intensité au centre qui vaut 1000. Si t est si petit ici, c’est juste pour pouvoir visualiser le tableau de chiffres complet plus bas, tableau nommé « Array[image,{t,t}] ». Mais pour les simulations que nous utiliserons pour obtenir les courbes, nous prendrons t typiquement qui vaut quelques centaines.
Note : dans ce qui suit, toutes les lignes de code de programme Mathematica seront présentées en couleur bleue.
t = 30; etoile = 20; planete = 4;
Array[image, {t, t}];
For[i = 1, i <= t,
For[j = 1, j <= t, r = N[Sqrt[(i – t/2)^2 + (j – t/2)^2]];
If[r > etoile/2, image[i, j] = 0,
teta = N[ArcTan[r/(etoile*100)]];
omega = N[ArcTan[(etoile/2)/(etoile*100)]];
image[i, j] =
N[IntegerPart[
1000*(0.3 +
0.93*Sqrt[(Cos[teta])^2 – (Cos[omega])^2]/Sin[omega] –
0.23*((Cos[teta])^2 – (Cos[omega])^2)/(Sin[omega])^2)]]; ]; j++;]; i++;];
Imprimons à présent la matrice numérique obtenue, qui est une sorte de disque stellaire numérique, les valeurs indiquant l’intensité lumineuse en leur position sur le disque. Cette intensité est maximale au centre et elle diminue en allant vers le bord en respectant la loi donnée plus haut :
Print[TableForm[Array[image, {t, t}], TableAlignments -> Automatic]]
Notes :
Le disque stellaire peut sembler elliptique, mais c’est une illusion. Il est circulaire et se présente ainsi juste parce que l’espacement entre les lignes et entre les colonnes n’est pas le même. Rien ne s’opposerait par contre à ce que nous fabriquions un disque stellaire numérique d’étoile aplatie aux pôles, comme Achernar !
L’intensité au centre est maximale : elle est de 1000. Il peut paraître curieux que l’intensité de bord varie tant : de 300 à 653. Mais cela est dû au trop faible nombre de « pixels » de l’image de l’étoile. La simulation réelle fonctionne avec une bien plus grosse matrice et les nombres de l’intensité du bord du disque varient dans une fourchette bien plus restreinte.
Cela dit, la loi d’assombrissement centre-bord de l’intensité lumineuse n’est peut-être pas la meilleure et la conversion que je fais pour passer de θ et de Ω à r et R peut être discutable, comme annoncé plus haut…
Si nous voulons à présent rajouter une tache stellaire par exemple au centre de ce disque stellaire, il nous suffit de rajouter une zone avec des 0. Voici un tel exemple de disque stellaire avec tache solaire carrée au centre. Bien entendu, une telle forme de tache n’existe pas dans la nature, mais on peut reproduire le type de tache que l’on veut et même avec un effet « pénombre » si on le désire : il suffit de mettre des nombres plus grands que 0 (très noir) et d’autant plus clairs que l’on se rapproche de 1000, la clarté maximale ici. Mais on pourrait coder les niveaux de gris, ou plutôt les niveaux de luminosité en allant de 0 à 1000000 par exemple.
Lignes de code pour rajouter une tache stellaire carrée au centre du disque stellaire :
For[i = IntegerPart[t/2 – 3*etoile/100],
i <= IntegerPart[t/2 + 3*etoile/100],
For[j = IntegerPart[t/2 – 3*etoile/100],
j <= IntegerPart[t/2 + 3*etoile/100], image[j, i] = 0; j++;];
i++;]
Ici, on rajoute une tâche carrée dont la taille est typiquement de 7 centièmes d’un diamètre stellaire.
Voici la nouvelle matrice numérique ainsi obtenue :
3) Calcul de points de la courbe de lumière du transit
Calculons à présent l’intensité lumineuse totale de l’étoile (variable « inttot »). Cette opération revient à calculer la somme de tous les éléments de la matrice :
inttot = 0;
For[i = 1, i <= t, For[j = 1, j <= t, inttot = inttot + image[i, j];
j++;]; i++;];
Print[inttot];
Enfin, faisons passer la planète devant l’étoile.
Array[courbe, t];
For[c = 1, c <= t, courbe[c] = inttot; c++;];
For[x = -t/2 + planete/2 + 1, x <= t/2 – planete/2,
y = 0*x; ix = IntegerPart[x + t/2]; jy = IntegerPart[y + t/2];
Print[« x= », x, » y= », y, » ix= », ix, » jy= », jy];
intmoins = 0;
For[i = ix – planete/2, i <= ix + planete/2 – 1,
For[j = jy – planete/2, j <= jy + planete/2 – 1,
If[(i – ix)^2 + (j – jy)^2 <= (planete/2)^2,
intmoins = intmoins + image[i, j]]; j++;]; i++;];
courbe[ix] = inttot – intmoins;
x++;];
Print[Array[courbe, t]];
ListPlot[Array[courbe, t]]
On définit ici un tableau à une dimension « Array[courbe,t] » de taille t, et l’on initialise au préalable toutes ses valeurs à l’intensité maximale de l’étoile « inttot ».
On se contente ensuite de faire se déplacer le centre de la planète sur une droite de coordonnées (x,y) dont on entre l’équation : ici on a y=0, mais on pourrait rentrer à la place n’importe quelle équation de droite y=ax+b. Pour faire cela, on se déplace sur l’abscisse x pas à pas, en faisant varier cette abscisse à chaque fois de un seul « pixel » représenté par un seul élément de notre matrice. Et on calcule pour chacune de ces positions x, une intensité lumineuse à enlever « intmoins » en ne considérant que les « pixels » dans le carré de côté le diamètre de la planète et de centre (x,y). Mais on n’enlève pas tous les pixels de ce carré, notre planète étant circulaire, d’où le rajout du test « if » qui permet de n’enlever que les pixels dont la distance au point (x,y) est inférieure au rayon de la planète. On ne touche ainsi jamais à la matrice du disque stellaire de départ, puisque pour chaque coordonnée (x,y) du centre de la planète, on calcule l’intensité à enlever représentée par un nombre unique, correspondant aux zones du disque stellaire masquées par l’étoile. Le programme tourne bien plus vite comme cela.
4) Aspect de la courbe du transit devant étoile sans tache stellaire centrale et avec tache stellaire centrale
Précisons avant de commencer la présentation des résultats de la simulation que tous les calculs ont à chaque fois duré moins de 2 minutes sur un PC de bureau usuel (calculs réalisés en mars 2013 !).
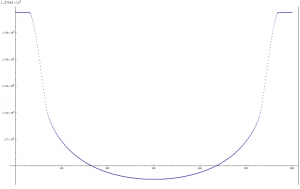
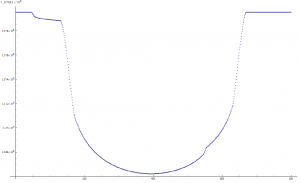
Pour la simulation ci-dessous, on prend une taille de matrice 600×600. Le diamètre de l’étoile est de 500 et celui de la planète de 40. On n’a pas mis de tache stellaire centrale ici. Et la planète traverse le disque stellaire de manière à ce que les deux centres des astres se confondent au milieu du transit. Dans la réalité, ce n’est presque jamais le cas et la trajectoire du transit serait matérialisée par une corde coupant le cercle « bord du disque » en des points non diamétralement opposés.
On notera que le « fond » de la courbe est vraiment très bombé. Un effet de mon interprétation de la loi d’assombrissement centre bord ?
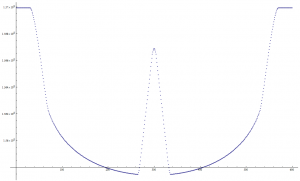
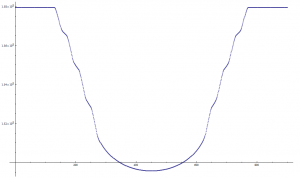
Refaisons la même simulation en ajoutant au centre une tache stellaire de taille 7 centièmes du diamètre du disque stellaire.
Bien entendu, si la tache est plus grosse que la planète, le pic central remonte jusqu’au « plateau » d’intensité maximale. Ce n’est pas le cas ici.
5) Aspect de la courbe du transit devant étoile d’une planète avec une grosse lune
Taille de matrice : 800×800.
Diamètre de l’étoile : 500.
Diamètre de la planète : 40.
Diamètre de sa lune : 10.
Distance planète-lune : 100.
La lune précède la planète dans le transit.
On commence donc par avoir une faible baisse de luminosité avec fond non plat.
Ensuite, dès que la planète commence son transit, la baisse de luminosité principale se creuse, toujours avec fond non plat.
Lorsque la luminosité remonte, on voit une perturbation : une petite augmentation de luminosité du fait que la lune cesse de transiter devant l’étoile avant la planète.
Voici un aspect de courbe de lumière que pourrait avoir un transit de planète avec une lune.
Bien entendu, une courbe de lumière d’un transit de planète avec une lune pourrait avoir bien des aspects différents en fonction de la distance apparente planète-lune qui pourrait aussi être supérieure au diamètre apparent du disque stellaire. Dans ce cas par exemple, on aurait deux cuvettes séparées : une peu profonde, celle de la lune ; et une plus profonde, celle de la planète.
Mais notre but ici n’est pas de montrer tous les cas possibles, il y en a bien trop…
6) Transit devant une étoile sans tache d’un objet en forme de « code barre »
Cette idée n’est pas de moi, mais de notre vénérable Président d’Honneur Luc Arnold. Il est fait mention de ses travaux dans le Hors série N°19 de Ciel et Espace de juillet 2012 « Extraterrestres, où sont-ils ? ».
Luc signale dans l’article qu’alors qu’il essayait précisément de modéliser numériquement un transit d’exoplanète, il s’était trompé dans la forme du corps passant devant l’étoile.
Il a ensuite expliqué que cela lui a donné l’idée de tester des objets transitant devant les étoiles mais de forme autre que circulaire. Il a essayé les triangles équilatéraux, les carrés…
Mais la forme la plus concluante était, selon l’article une sorte de code barre.
J’ai moi-même essayé. J’écris ces lignes sous contrôle de Luc Arnold.
Taille de matrice : 900×900.
Diamètre de l’étoile : 500.
Objet occulteur : sorte de « code barre », 4 barres de largeur 20 espacées de 20, de longueurs 100.
Voici le résultat de la simulation !
7) A quoi servent ces simulations numériques ?
Lorsqu’on fait une mesure réelle de transit d’exoplanète, on obtient en général une courbe qui ressemble à la première que nous montrons dans cet article.
Mais grâce à la modélisation numérique, on peut constituer une base de données avec une gamme complète de courbes en faisant varier tous les paramètres : diamètre relatif étoile-planète, loi d’assombrissement centre-bord du disque stellaire et autres…
Il « suffit » alors de trouver dans cette base de données la courbe simulée qui « colle » le mieux à celle mesurée pour retrouver les paramètres du système réel planète-étoile du transit !
Mais moi-même, je ne saurais pas écrire un programme qui trouve la courbe théorique la plus ressemblante à la mesurée. Ce doit être un travail de statisticien !
La dernière courbe du passage devant l’étoile de l’objet en forme de « code barre », montre qu’une civilisation technologiquement avancée et capable de construire un tel masque, pourrait ainsi révéler sa présence aux autres civilisations, à condition que ces dernières aient la bonne idée de faire de la photométrie stellaire.
Bien entendu, le travail présenté ici ne prétend pas être un travail de professionnel. D’ailleurs, les simulations numériques de transits d’exoplanètes faites par les professionnels doivent probablement être bien plus fines et considérer bien plus de paramètres que ce qui est fait ici.
Néanmoins, cet article, je l’espère, a le mérite de faire comprendre le principe de la modélisation numérique des transits d’exoplanètes et d’expliquer aussi leur utilité et comment grâce à eux, on peut en apprendre sur un système planétaire mesuré réellement.
Et je dois bien avouer que je me suis bien amusé à écrire ces petits programmes…
Mais il faudrait étudier la loi d’assombrissement centre bord de l’intensité lumineuse d’un disque stellaire de manière plus rigoureuse pour améliorer la qualité de la modélisation numérique.