En un lieu terrestre donné, sont visibles plus d’éclipses de Lune que de Soleil. Il semble alors légitime de croire, ou de penser, qu’il y a plus d’éclipses lunaires que solaires, mais ceci est inexact à l’échelle globale de la Terre. Au cours d’un saros, on compte 32 éclipses solaires vs 23 éclipses lunaires. Pour ce décompte, on considère uniquement les éclipses du canon d’Oppolzer : les éclipses totales ou partielles du Soleil ; les éclipses totales ou partielles de la Lune par l’ombre de la Terre. Ne sont pas répertoriées les éclipses de Lune par la pénombre car elles sont peu visibles et n’ont rien de spectaculaire. Le saros est le cycle qui gère la répétition des séries d’éclipses. Ce cycle était déjà connu dans l’antiquité, bien avant notre ère. Il dure 6 585,32 jours, c’est-à-dire 223 lunaisons. On dit généralement 18 ans 11 jours et 8 heures, mais s’il y a 5 années bissextiles dans les 18 années, le complément n’est alors que de 10 jours et 8 heures pour finir le saros.
Pourquoi, en un lieu donné, voit-on plus d’éclipses lunaires que solaires ?
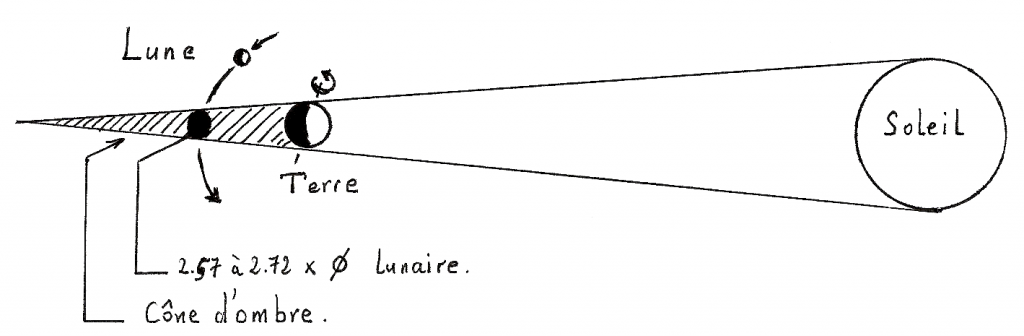
Une « éclipse lunaire » est le passage total ou partiel de la Lune dans le cône d’ombre de la Terre. Elle est donc visible simultanément par tout le demi-globe terrestre qui fait face à la Lune. Le cône d’ombre de la Terre peut contenir en moyenne 2,6 fois la Lune, en fait entre 2,57 fois et 2,72 fois en raison des distances variables du Soleil et de la Lune (figure 1). Entre le premier et le dernier contact, il peut s’écouler jusqu’à presque 5 heures dans les cas les plus favorables. Pendant ce temps, la Terre continue de tourner sur elle-même, à raison de 15° par heure. De ce fait, la visibilité de l’éclipse concerne beaucoup plus que la moitié du globe terrestre, jusqu’à 60 % environ. Bien sûr, certains ne verront que le début du phénomène, car la Lune se couche pendant le déroulement de l’éclipse, alors que d’autres ne verront que la fin, car la Lune se lève quand l’éclipse est déjà commencée. Il reste tout de même une grande partie du globe pouvant assister au phénomène du début à la fin. En un point terrestre donné, la probabilité de voir au moins en partie une éclipse lunaire est donc de l’ordre de 0,6. Soit une bonne dizaine d’éclipses par saros.
Une « éclipse solaire » est l’occultation partielle, totale ou annulaire du Soleil par la Lune. Les différentes heures (contacts, début et fin de la totalité ou annularité le cas échéant, maximum) ainsi que la « grandeur » pour une éclipse partielle sont autant d’éléments déterminés localement. Aucune de ces données n’est universelle. La zone éventuelle pour laquelle l’éclipse est totale, annulaire ou mixte dessine une bande, curviligne en raison essentiellement de la rotation de la Terre, pouvant atteindre quelques milliers de kilomètres de long, sur quelques 100 à 200 km de large, 300 km au maximum dans les cas les plus favorables.. Autant dire une surface quasiment nulle par rapport à celle du globe. Donc en un lieu donné, la probabilité de voir une éclipse totale ou annulaire est quasiment nulle. Pour mémoire, rappelons les 2 dernières éclipses totales que j’ai pu observer en France. Celle de 1961 était totale là où j’habitais à l’époque, à Puyméras, petit village du nord du Vaucluse, mais elle était partielle à Wittelsheim. Celle de 1999 était totale à Strasbourg, la ligne de centralité étant un peu plus au nord, mais elle n’était que partielle à Wittelsheim. Je ne suis pas arrivé à trouver, sur le « net », la date de la dernière éclipse totale à Wittelsheim. Pourtant j’ai remonté les archives sur plus de 2 siècles. Autour de la zone de totalité ou d’annularité, l’éclipse est partielle. La « grandeur de l’éclipse », i.e. la proportion du diamètre solaire caché, diminue selon un gradient assez rapide. La zone où l’éclipse est vue partielle a des dimensions très variables selon les fois, mais représente en moyenne et environ 8 % du globe. En un point terrestre donné, la probabilité de voir une éclipse solaire partielle est de l’ordre de 0,08. Soit 2 à 3 éclipses par saros.
Pourquoi y a-t-il globalement plus d’éclipses solaires que lunaires ?
Ceci est dû à la parallaxe de la Lune.
Pour se faire une bonne idée de ce qu’est la parallaxe, faites donc la petite expérience suivante. Votre pouce étant tendu à bout de bras, observez-le successivement de l’œil gauche puis de l’œil droit. Vous le voyez se déplacer de droite à gauche par rapport au fond de la salle dans laquelle vous êtes installé. Refaites la même manipe avec le pouce bien plus près… En apparence, il se déplace davantage. Je dis bien en « apparence » car ce n’est pas le pouce qui se déplace, c’est la direction de visée par rapport au « lointain », le fond de la salle pour cette expérience.
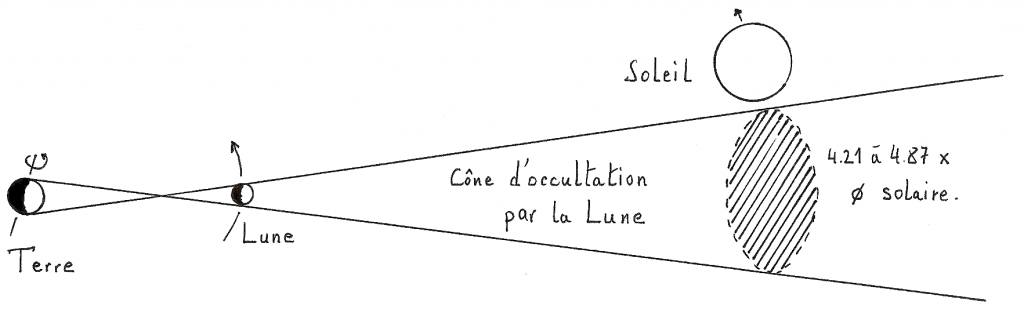
La Lune est relativement proche de la Terre. Si on l’observe, en un même instant, à partir de lieux terrestres différents, elle n’est pas vue dans la même direction de visée. Suite à cette parallaxe, le cône « d’occultation possible » par la Lune découpe à la distance du Soleil un disque qui peut contenir en moyenne 4,5 fois le Soleil, en fait entre 4,21 fois et 4,87 fois en raison des distances variables (figure 2). Bien plus que les 2,6 fois la Lune dans l’ombre de la Terre. On conçoit alors aisément qu’il y ait plus d’éclipses solaires que lunaires.
Successions des éclipses d’un saros, décompte dans le canon d’Oppolzer.
On a quelques éclipses solaires ou lunaires isolées. Mais le plus souvent, deux éclipses solaire et lunaire se suivent avec un décalage d’une demi-lunaison. Il existe même des successions de 3 éclipses : Soleil-Lune-Soleil, mais jamais Lune-Soleil-Lune. En effet, comme on vient de l’expliquer, l’alignement des 3 astres a besoin de moins de précision pour une éclipse solaire que pour une éclipse lunaire.
| Soleil | Lune | |
| 9 fois S | 9 | |
| 2 fois L | 2 | |
| 9 fois S – L | 9 | 9 |
| 10 fois L – S | 10 | 10 |
| 2 fois S – L – S | 4 | 2 |
| 0 fois L – S – L | ||
| Total | 32 | 23 |
En moyennes arrondies :
– La NL occulte le Soleil 1 fois sur 7. (14,3 % des NL).
– La PL s’éclipse dans l’ombre de la Terre 1 fois sur 10. (10,3 % des PL).