Le but de cet article n’est pas tant de calculer les données physique du jeu Animal Crossing new horizons que de montrer que la science dite dure, n’est pas nécessairement austère et peut être fun. La démarche suivie se veut scientifique, elle peut-être critiquée, corrigée ou reproduite.

Attention, cet article contient des vidéos pouvant dévoiler des étapes du jeu et nuire à l’expérience vidéoludique.

Animal Crossing new horizons (ACNH) est un jeu vidéo de simulation de vie édité par Nintendo. Sorti en 20 mars 2020, il a été vendu à 37 millions d’exemplaires. Le-a joueur-euse incarne un personnage qui évolue sur une île déserte. On se rend rapidement compte que la « planète » a une forme cylindrique, du moins, pour les parties auxquelles le-a joueur-euse a accès. Du coup, il est difficile d’appeler ce monde une planète qui par définition doit être ronde ! Le cylindre-monde donc, est systématiquement allongé face à la caméra (ci-dessous le trailer d’ACNH, et une vidéo du jeu). On se propose ici de calculer les propriétés de ce monde cylindrique.

Vidéo de présentation officielle d’ACNH :

Visualisation de la forme cylindrique d’une île :

Calculer le rayon du monde ACNH

Le plus simple pour obtenir le monde serait de pouvoir le mesurer directement. Il faudrait d’abords avoir une règle, pour cela, on peut assumer que les personnage sont aussi grand que dans notre monde, disons que l’avatar de le-a joueur-euse mesure 1,75 m. Et ensuite pouvoir dézoomer pour avoir le diamètre complet du cylindre-monde, mais ça, c’est impossible !

Ce n’est pas grave, on va trouver un autre moyen. Gardons notre règle et mesurons un élément qui dépend de la rotondité du cylindre-monde. Par exemple, à quelle distance se trouve la ligne d’horizon. Trouvons un arbre, repérons son horizon et mesurons la hauteur de l’arbre et la distance entre l’arbre et son horizon.

La hauteur de l’arbre :

Pour calculer la hauteur de l’arbre, il nous suffit de le comparer avec notre personnage étalon et faire un produit en croix. Pouvant déplacer le personnage sur notre île, il est facile de le placer à la même distance de la caméra que l’arbre.

On a donc :

Notre arbre mesure donc 3,5 m

Distance de l’arbre à son horizon

Il n’est pas possible de mesurer directement la distance de l’arbre à son horizon. Mais il est possible de compter le nombre de pas nécessaire pour aller du pied de l’arbre à son horizon. Et ensuite de mesurer la longueur d’un pas.

Distance de l’arbre à son horizon (trait blanc) en nombre de pas :

Il y a 14 pas de l’arbre à son horizon et en refaisant la même méthode de calcul pour mesuré un pas que lorsqu’on a mesuré l’arbre, on trouve qu’un pas équivaut à 1 m. Il y a donc 14 m qui séparent l’arbre de son horizon.

Calcul du rayon du cylindre-monde

On a maintenant toutes les données nécessaires pour calculer le rayon du cylindre-monde grâce à Pythagore.

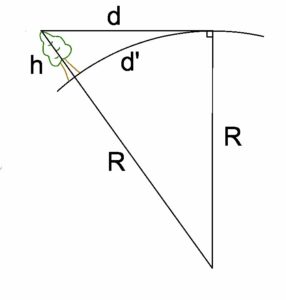
Sur le schéma, on a h la hauteur de l’arbre, R le rayon du cylindre, d la distance du sommet de l’arbre à l’horizon et d’ la distance du pied de l’arbre à l’horizon en suivant la courbure du cylindre.

Pythagore nous donne : (h+R)² = d² + R²

Que l’on peut simplifier en :

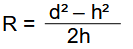
En remplaçant h par sa valeur de 3,5 m et en approchant d par d’, on trouve le rayon du cylindre monde égale à 25 m environ.

Avec 25 m de rayon, la circonférence, le tour du cylindre fait alors environ 160 m.

La taille de l’île

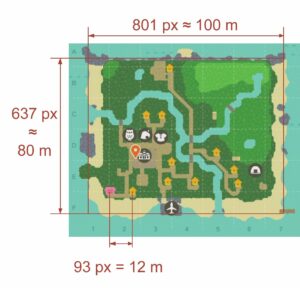
Un outil très pratique pour mesurer la taille de l’île est la carte de l’île disponible dans le jeu. Encore une fois, on va mesurer la distance entre deux points remarquables de la carte pour avoir une échelle. Prenons la distance entre deux maisons voisines.

Seul la distance entre les deux maisons situées au sud-ouest de l’île est facilement mesurable dans le jeu. Elle fait 12 pas. Or nous avons vu qu’un pas fait environ un mètre, on a donc notre échelle, la distance entre ces deux maison fais 12 m.

Dimension de l’île

Notre île fait donc environ 100 m par 80 m, soit 80 ares

Les autres dimensions du monde d’ACNH

La longueur du cylindre-monde

Il n’y a aucune information sur la longueur réelle du cylindre-monde. Néanmoins, un joueur peut voyager par avion sur l’île d’un autre joueur pour peu qu’il ait un code d’accès. On peut donc supposer que les îles de tous-tes les joueur-euse-s sont situé sur le même monde (ce qui rend le voyage par avion possible).

Il y a eu 37 millions de ventes d’ACNH, il y a donc tout autant d’île de même taille. En espaçant deux île par 50 m de mer, on obtient une distance minimale de 5 500 millions de mètres pour la longueur du cylindre-monde, soit 14 fois la distance Terre-Lune. Le monde contient aussi une myriade de petites îles innombrables que l’on peut visiter par bateau ou par avion. Il est impossible de quantifier ces îles, gardons juste en tête que la longueur obtenue est un minimum et non une valeur absolue. La vraie valeur peut facilement atteindre le double ou plus.

Le monde d’ACNH est donc un cylindre de 25 mètres de rayon et d’au moins 5,5 millions de km de longueur.

La masse volumique

Oulala ! On s’attaque a du lourd, là !

Comme on vient de le voir, le monde d’ACNH est très loin d’être une sphère. Il n’est donc pas possible d’assimiler le cylindre-monde à un unique point comme on en a l’habitude en astronomie.

Le théorème de Gauss gravitationnel permet de relier la masse volumique au champ de gravité et de nous sortir de là. Je passe le détail des calculs, ça passe par des intégrales de surface… Bref ! En supposant que le champ de gravité est identique à celui sur Terre, on finit par avoir :

C’est presque la densité d’une étoile à neutron !

Spéculation sur le monde d’ACNH

On a vu que le monde d’ACNH est un cylindre de 25 mètres de rayon, d’au moins 5,5 millions de km de longueur de 900 000 tonnes par m³. Un cylindre aussi fin pour une masse aussi élevé semble contradictoire. Ce ne l’est que si on considère le cylindre-monde comme étant naturel, mais rien dans le jeu ne permet de le conclure. Certes on trouve des fossiles sur l’île, ce qui prouve une certaine ancienneté à l’île. Mais est-ce suffisant pour conclure à une origine naturelle du monde d’ACNH. Il y a un détail qui vient mettre en branle cette origine naturelle de ce monde : le soleil.

Pour rappel, l’île s’étend sur la moitié de la circonférence du cylindre. Si il est possible qu’une étoile éclaire la moitié d’un cylindre, les ombres portées sur le cylindre doivent être radicalement différentes sur les extrémités opposées de l’île.

Or il n’en est rien, l’ombre est la même à une heure donnée.

Absence de déformation de l’ombre en se déplaçant perpendiculairement à l’axe du cylindre

Cela implique que la source de lumière se déplace dans le ciel pour suivre le personnage de le-a joueur-euse. L’absence d’ombres doubles indique que cette source lumineuse est unique et le personnage est l’unique habitant suivi par la lumière. Et c’est ainsi sur les 37 millions d’île, seul le personnage humain est éclairé. On est donc sur une construction spatiale de plusieurs million de kilomètres de long, capable de maintenir de la matière extrêmement dense spécialement conçu pour des millions d’êtres humains.